X²- test   (testování shody rozdělení četností)

 

Většina postupů  při zpracování souborů dat  ve statistice se liší podle toho, jestli daný soubor  má nebo nemá GNR. V biologii většinou toto  rozdělení předpokládáme, nemusí však  být vždy. Na podmínku normality jsou citlivé hlavně některé statistické testy, které  používáme k  hodnocení souborů  (při n  > 30  se citlivost zmenšuje).

Pro rozhodnutí, zda se rozdělení četností v souboru shoduje s předpokládaným GNR  se nejčastěji používá X²test  dobré shody.

Je  založen na  posouzení rozdílu  mezi skutečnými  (empirickými) četnostmi výskytu hodnot ve  VS a očekávanými (teoretickými) četnostmi,  odpovídajícimi  příslušnému  rozdělení  pravděpodobností (GNR).

(X²test rozhoduje, zda je  rozdíl mezi empirickými a teoretickými četnostmi způsoben pouze náhodně  a VS odpovídá GNR, nebo je rozdíl natolik velký, že je způsoben tím, že VS nepochází z populace odpovídající GNR, ale z nějakého jiného rozdělení.)

 

 

Např.:  při sledování  hmotnosti králíků  máme rozhodnout, zda náhodný  výběr o  1000 kusech  odpovídá GNR  s těmito  parametry: m =3.75 kg , s = 0.5 kg (kterým se řídí celá populace - ZS).

Při testu vycházíme z těchto hodnot:

 VS :  x₁, x₂, x₃, ..... x₁₀₀₀  (n = 1000)

 ZS :  m =3.75, s =0.5

 

1)        Zvolí se intervaly tříd  (d_i - dolní mez, h_i - horní mez) , např.po 0.5 kg            

          (  _i - číslo třídy   )

2)        Zjistí  se absolutní četnost empirická – n_ei  v jednotlivých    třídách ( => histogram výběrového souboru).

3)        Vypočítá se absolutní četnost teoretická (očekávaná pro GNR) -  n_oi  v jednotlivých třídách :

 

a)       pro hodnoty d_i a h_i se vypočítají relativní hodnoty u_di a  u_hi :

                              

b)      pro  u_di a u_hi  se zjistí v  tabulkách hodnoty distribuční  funkce :  F(u_di),  F(u_hi)

c)       pro každou třídu se zjistí teoretická pravděpodobnost :
                                       p_oi = F(u_hi) - F(u_di)

d)      pro každou třídu se vypočítá očekávaná absolutní četnost :     n_oi = n . p_oi

4)        Vypočítá se testová charakteristika X² :

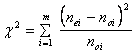                                                   m – počet tříd

5)        Vypočítaný X² porovnáme s tabulkovou hodnotou  X²_(a,n)  -   kritická hodnota při          pravděpodobnosti chyby a (např.0.05) a  n stupních volnosti (n = m-k-1).
      k – počet parametrů GNR, které neznáme, a musíme je odhadnout z VS.

 

6)        Je-li  X² £  X²_(a,n)  => statisticky nevýznamný  rozdíl mezi empirickou  a teoretickou četností, způsobený náhodnými činiteli; (VS odpovídá GNR).

 

Je-li  X² > X²_(a,n) => statisticky významný rozdíl mezi nei a noi, způsobený tím, že VS odpovídá jinému rozdělení než  GNR (rozdíl není způsoben jen náhodnými činiteli).

Pro charakteristiku a další testování takového VS je nutno použít jiné rozdělení a neparametrické metody.