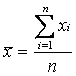
Example No.10
Enter data:
Urine ABE (xi) : 20, 10, 50, 90, 135, 150, 173, 195, 205, 229 [mmol.l-1]
Urine pH (yi): 7.0, 7.2, 8.0, 7.6, 7.9, 8.3, 8.0, 8.1, 8.6, 8.1 [-log H+]
1) Calculation of mean values:
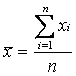
Results: Urine ABE: 138.1818 mmol.l-1
Urine pH: 7.89091
2) Calculation of coefficients in equation of linear regression (y=bx + a):
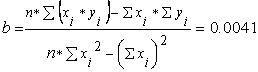
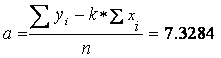
Result: Linear regression y = 0.0041x + 7.3284
3) Calculation of the correlation coefficient r:

4) Calculation of significance of the correlation coefficient:
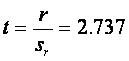
 DF = n-2 = 9
DF = n-2 = 9
As calculated t > tcrit= 2.262 (DF=9, α=0.05) the correlation coefficient is statistically significant.
Conclusion: between ABE and pH of urine the relation was found that is described by means of linear regression y=0.0041x + 7.3284 and correlation coefficient 0.75223 that is statistically significant (p<0.05).
Note:
Both variables monitored in this example are equally valuable, then its relation is reciprocal (correlative relation) and it is possible to evaluate it also by means of the method, based on the mutual exchange of data sets (X« Y).