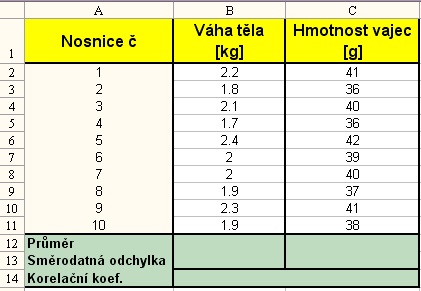
MS Excel - příklad 12
1. Zadání hodnot sledovaných veličin do tabulky (buňky B3:B13 a C3:C13); pro výpočet korelačního koeficientu v buňce B14 vyvolat menu Vložit funkci - Statistické - CORREL:

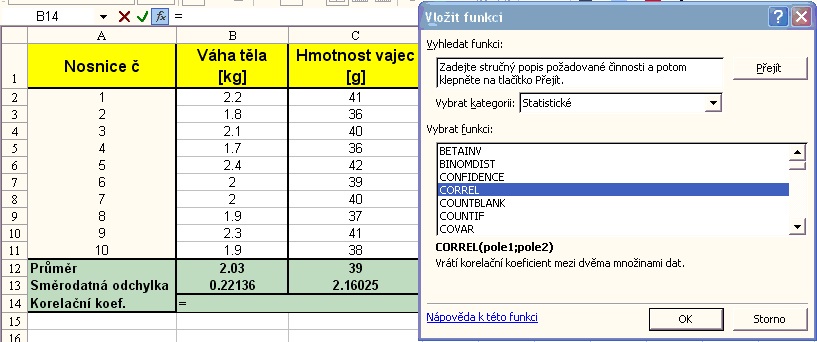
2. V dialogovém okně zadat do Pole1 (příp. Matice1 - podle verze MS Excel) rozsah buněk veličiny Váha těla (B2:B11) a do Pole2 (Matice2) rozsah buněk veličiny Hmotnost vajec (C2:C11). Výsledek je zobrazen po stisku tlačítka OK. Výsledek výpočtu: hodnota korelačního koeficientu = 0.95266 (silná přímá závislost):

3. Grafické znázornění závislosti včetně výpočtu lineární regresní funkce: po označení buněk B2:C11 vyvolat menu Průvodce grafem - volba Typu grafu - XY bodový:
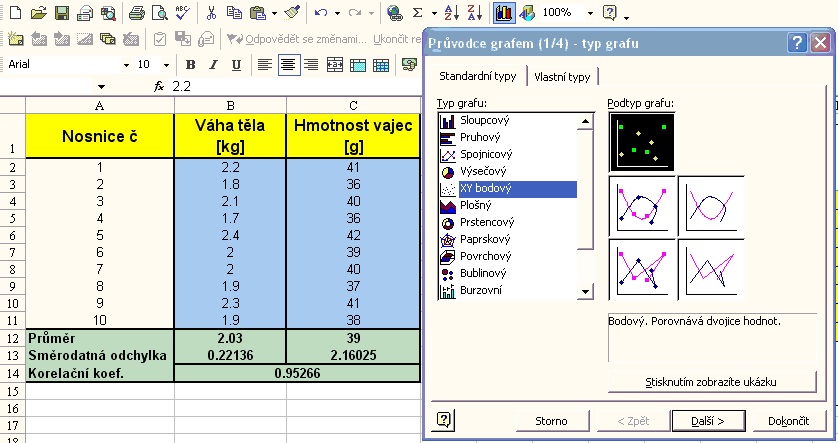
4. Zobrazení náhledu grafu v druhém dialogovém okně:
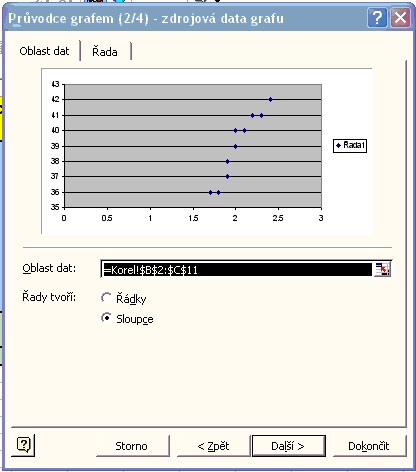
5.Zadání názvu grafu a popisků osy X aY:
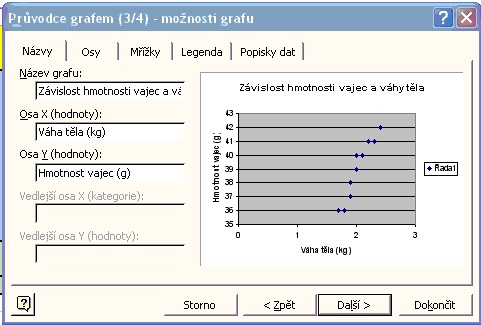
6. Volba umístění grafu - Jako objekt do: (aktuální list):
7. Po dokončení tvorby grafu lze upravit měřítko osy X pomocí kontextového menu (pravé tlačítko myši na ose X):
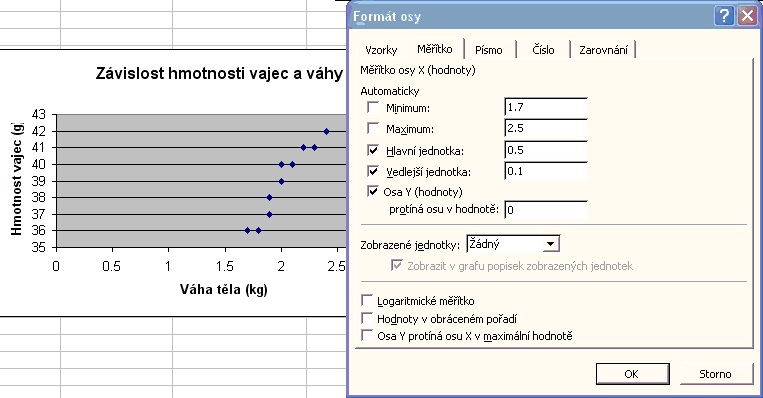
8. Proložení znázorněných bodů přímkou pomocí kontextového menu na libovolném bodě bodového diagramu - volba Přidat spojnici trendu - Typ: Lineární:
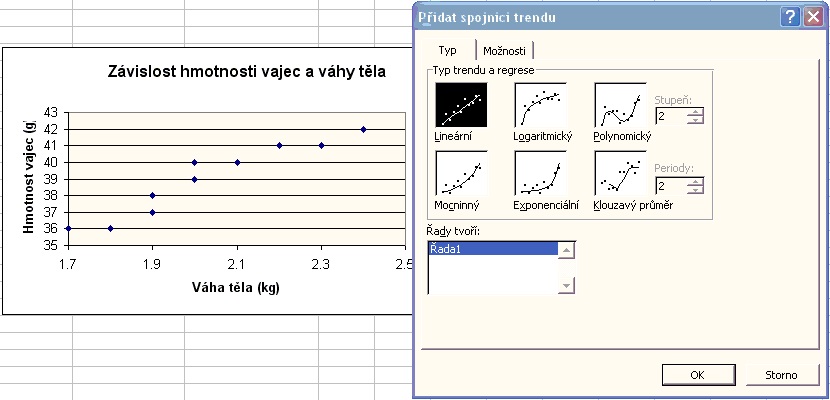
9. Zobrazení odpovídající rovnice lineární regrese - nabídka Možnosti - Zobrazit rovnici regrese:
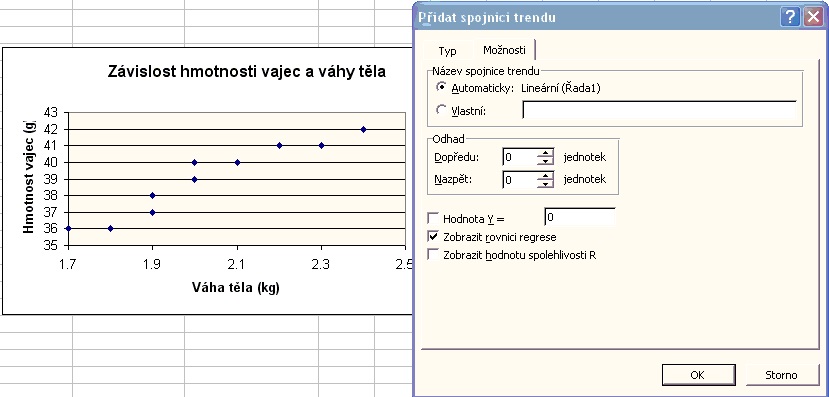
10. Dokončení grafického znázornění závislosti sledovaných veličin - tlačítko OK:
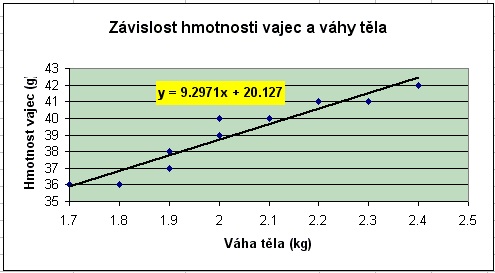
11. Závěr: Mezi váhou těla a hmotností vajec u nosnic byla zjištěna závislost, kterou lze popsat pomocí lineární regresní funkce y=9.2971x + 20.127 a korelačního koeficientu 0.95266.
Poznámka:
Obě sledované veličiny v tomto příkladu jsou víceméně stejnocenné, jejich závislost je tedy vzájemná (korelační vztah) a proto ji lze hodnotit i postupem, založeným na vzájemné výměně souborů dat (X« Y).