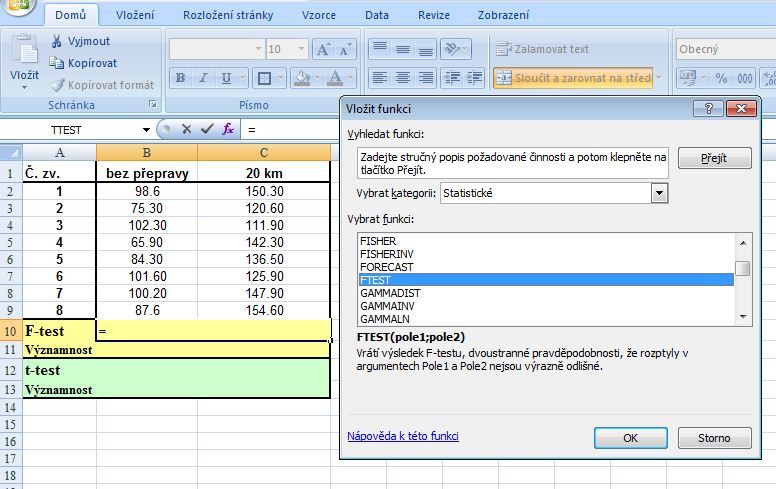
MS Excel - příklad 17
1. Zadání hodnot výběrových souborů do tabulky (buňky B3:B12 a C3:C12); pro výpočet F-testu v buňce B15 vyvolat menu Vložit funkci - Statistické - FTEST (před nepárovým t-testem pro zjištění rozdílu mezi průměry souborů je nutno nejprve otestovat rozdíl rozptylů pomocí F-testu):

2. V dialogovém okně zadat do pole Pole1 (příp. Matice1 - podle verze MS Excel) rozsah buněk výběrového souboru bez přepravy - B3:B12 a do Pole2 (Matice2) rozsah buněk výběrového souboru 20 km - C3:C12 (lze označit pomocí myši v tabulce). Výsledek je zobrazen po stisku tlačítka OK:
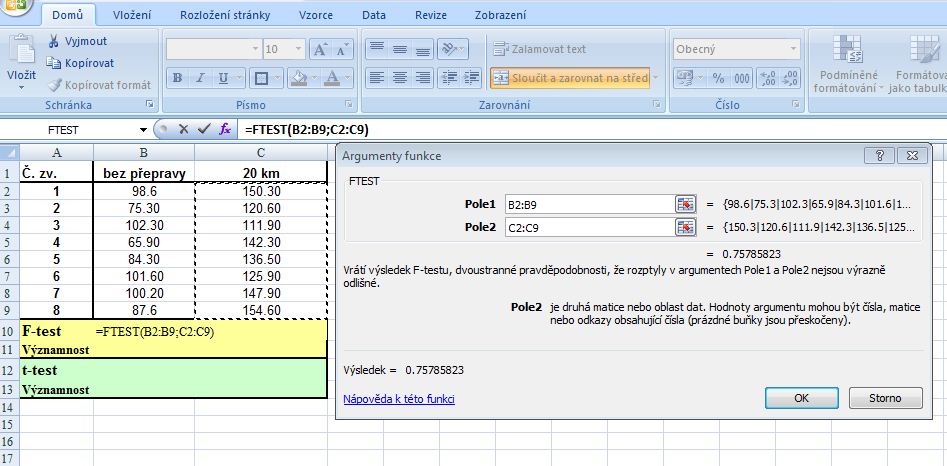
3. Výsledek F-testu: p=0,75786 představuje pravděpodobnost nulové hypotézy o shodě rozptylů obou souborů (pravděpodobnost chyby a), tzn. že mezi rozptyly souborů byl zjištěn statisticky nevýznamný rozdíl. Výpočet nepárového t-testu pro otestování rozdílu průměrů obou souborů: v buňce B17 vyvolat menu Vložit funkci - Statistické - TTEST:
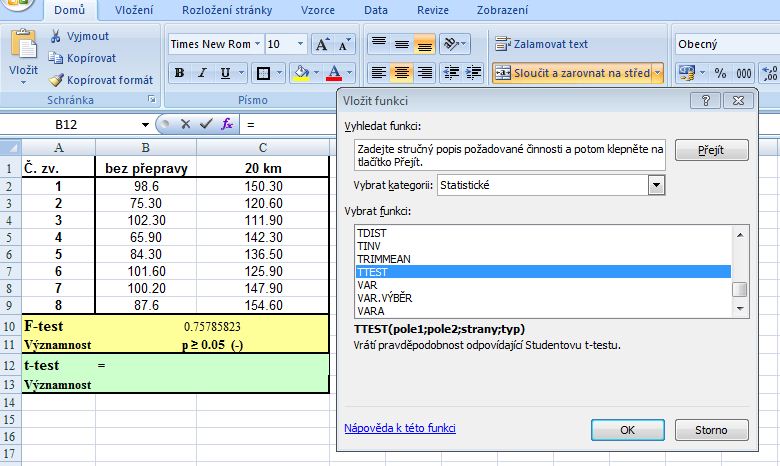
4. V dialogovém okně zadat do Pole1 (Matice1) rozsah buněk výběrového souboru bez přepravy - B3:B12 a do Pole2 (Matice2) rozsah buněk výběrového souboru 20 km - C3:C12 (lze označit pomocí myši v tabulce). Do řádku Strany (příp. Chvosty - podle verze MS Excel) zadat 2 (dvojstranný t-test) a do řádku Typ zadat 2 (podle výsledku předchozího F-testu: dva výběry se shodným rozptylem). Výsledek je zobrazen po stisku tlačítka OK:
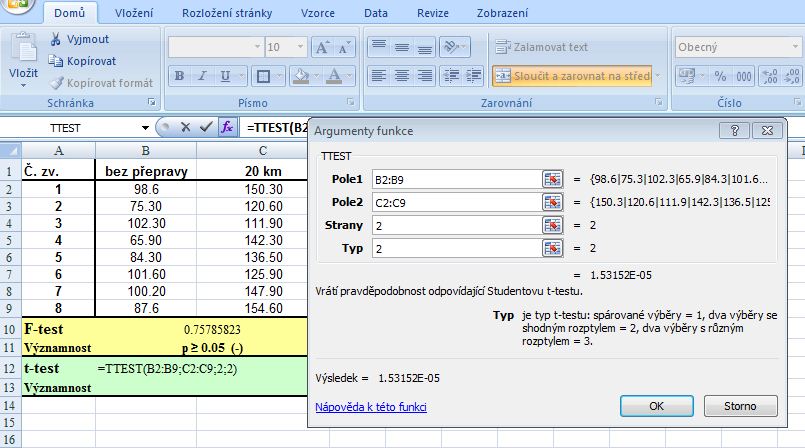
5. Zobrazení výsledků výpočtů:
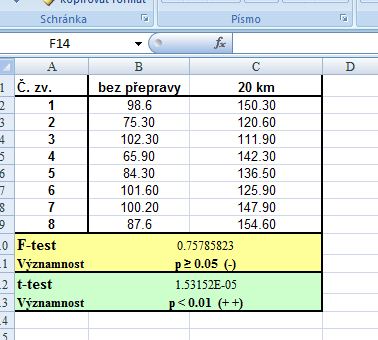
6. Výsledek t-testu: p=1,52152E-5 (=0,0000152152) představuje dvoustrannou pravděpodobnost nulové hypotézy o shodě středních hodnot obou souborů (pravděpodobnost chyby a). Protože je tato pravděpodobnost p < 0,01, znamená to, že rozdíl mezi testovanými středními hodnotami je statisticky vysoce významný (zamítáme nulovou hypotézu o shodě středních hodnot na hladině významnosti p = 0,01)
Závěr: Transport prasat na vzdálenost 20km vyvolává statisticky vysoce významné (p < 0,01) zvýšení koncentrace kortizolu v krevní plazmě prasat, což naznačuje vysokou hladinu stresové zátěže u prasat vlivem přepravy na tuto vzdálenost.