Analýza kategoriálních dat

Při sledování kvalitativních statistických znaků a následné analýze kategoriálních dat vycházíme z pravděpodobnosti výskytu daného znaku v populaci a z četností jedinců odpovídajících jednotlivým kategoriím (kvalitativním třídám) sledovaného nominálního znaku ve výběrových souborech. Získané četnosti (kategoriální data) zachycujeme pomocí jedno-, dvou- nebo vícerozměrných tabulek četností (případně relativních četností, procent). Každý rozměr (dimenze) tabulky odpovídá klasifikaci do kategorií podle určitého kvalitativního znaku.

Při zkoumání četností kategoriálních dat stojíme před podobnými úkoly jako v případě numerických dat u kvantitativních znaků. Můžeme porovnávat četnosti výskytu sledovaného kvalitativního znaku ve výběrovém souboru, se statistickou pravděpodobností výskytu tohoto znaku, která je teoreticky známá pro celou populaci. Můžeme také porovnávat četnosti výskytu sledovaného znaku mezi dvěma, případně i více výběrovými soubory nebo zjišťovat sílu závislosti jednotlivých kvalitativních znaků mezi sebou.

Základním statistickým postupem, který je nejčastěji využíván při analýze kategoriálních dat je c²-test (Chí kvadrát test) pro testování rozdílů četností (jak mezi soubory, tak i pro zjišťování závislosti kvalitativních znaků).

Při výpočtech spojených s analýzou kategoriálních dat pomocí c²-testu používáme s následujícím označením četností:

 n_e - empirická (pozorovaná) četnost výskytu znaku (platí pro výběrový soubor)

 n_o - očekávaná (teoretická) četnost výskytu znaku (platí pro populaci)

Poměr empirické četnosti výskytu znaku ve výběrovém souboru k celkovému počtu jedinců ve výběru představuje relativní četnost znaku (empirickou pravděpodobnost výskytu daného znaku - p_e):

Při nekonečném zvětšování rozsahu výběrového souboru n dostaneme v limitě tzv. statistickou (teoretickou) pravděpodobnost výskytu znaku - p_o (očekávanou pravděpodobnost, předpokládanou pro celý základní soubor). Pro nekonečně velký počet jedinců v populaci (N = ¥) nelze statistickou pravděpodobnost prakticky vypočítat, můžeme ji pouze odhadovat na základě empirické pravděpodobnosti. Čím větší je počet jedinců ve výběrovém souboru, na kterém provádíme sledování, tím více se hodnota empirické pravděpodobnosti (p_e) blíží k skutečné hodnotě teoretické pravděpodobnosti (p_o):

Testování rozdílů četností se (obecně) provádí c²-testem. Rozdíl mezi empirickými (pozorovanými) a teoretickými (očekávanými) četnostmi zachycuje testovací statistika, která má tvar:

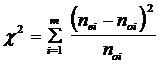
kde

m = počet kvalitativních tříd (kategorií) představujících varianty kvalitativního znaku

n_ei = empirická četnost (data z výběrového souboru)

n_oi = očekávaná četnost (teoretická, známá pro základní soubor)

 Protože platí, že ne= pe . n  a  no= po . n , lze použít i výraz :

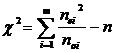
Je-li vypočtená statistika c² = 0, znamená to, že pozorované a teoretické četnosti jsou přesně stejné. Čím větší je hodnota c², tím větší je nesouhlas mezi empirickou (n_e) a teoretickou (n_o) četností v jednotlivých třídách.

Pro posouzení statistické významnosti rozdílu srovnávaných četností porovnáme vypočtený c² s tabulkovou kritickou hodnotou c²_{1-a (n)}. Jako kritické hodnoty pro c²–test slouží 1-a kvantily c² - rozdělení při n = m-1 stupních volnosti (viz Tabulky: Kritické hodnoty rozdělení c²).

Pokud vypočtená statistika (testovací kritérium) c² přesáhne tabulkovou kritickou hodnotu c²_{1-a (n)}, prohlásíme, že pozorované četnosti n_ei nesouhlasí statisticky významně s teoreticky očekávanými četnostmi n_oi  na hladině významnosti a.

Zpět